Clearly the construction of Obaminoes required a wealth of counting; sorting and classifying; measurement; coordinate geometry; symmetry; patterns and reasoning tools, skills, and problem solving. All of these areas are central parts of the Mathematics curriculum. And these issues pervade the planning, preparation, and final assembly of Obaminoes.
We give one specific example here, the labeling of the tiles that are used to construct the full mosaic. Because we needed to label the sections, a natural way to do this is to use coordinate geometry with the lower, left corner as the origin:
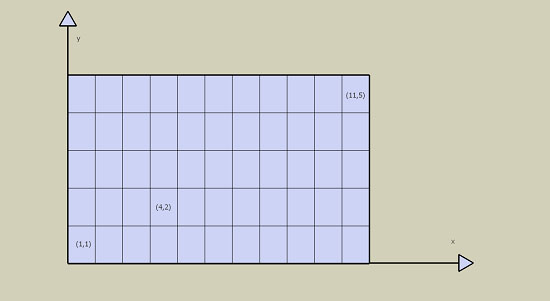
We also note that the construction of a suitably strong base for the mosaic involved a number of mathematics, physical, and woodworking challenges. What was needed was a light, strong base that supported the weight and resisted stress. In many ways this is the same situation faced by aviation and aeronautical engineers when designing wings of airplanes. Airplane wings are universally made with a skeleton that is composed of intersecting structural lengths that form strong lattice. This lattice is then covered with a strong skin that aids in the structural stability and directs airflow. Hollow core doors are made in a similar way, providing light, strong, and torsion-free doors.
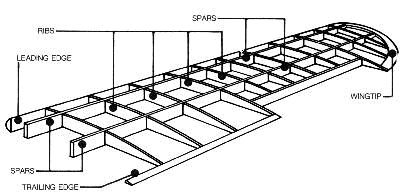
In woodworking a similar approach is used to make very strong boxes and bases - called torsion boxes. Three torsion boxes were constructed for Obaminoes. Each was 48" tall, either 21" or 28" wide, and 2 3/8" thick. The ribs were constructed from 1/2" medium density fiberboard of lengths of about 6" and 8" in the two directions. These were glued end to end with white wood glue. The skin was made by sheets of 3/16" hardboard.
In mid-May Prof. Fleron visited the school to talk to students in groups about these issues. A handout for students, parents, faculty and staff is available as a pdf:
Photos from this discussion are below:

